Research
HIV Modeling (Postdoctoral Work)
From 2014-2015 I contributed to the design, development, and statistical validation of a detailed stochastic and spatial model of the HIV epedemic. As part of this work, I oversaw the design and implementation of the “cascade of care” component of the model that simulates an individual’s interaction with a geographically local healthcare system. Recently I have begun work on developing and comparing algorithms and techniques to calibrate stochastic epidemiological models to observed data. I am particularly interested in metamodeling, experiment design, and sampling techniques rooted in Bayesian statistics.
Synthetic Biology (Ph.D. Work)

Dissertation
Programming Molecules and Cells: Design Architectures for Chemical Reaction and Gene Regulatory Networks. Submitted March 7, 2014.
Committee members: Eric Klavins (Chair), Georg Seelig, James Carothers, Mark Oskin (GSR)
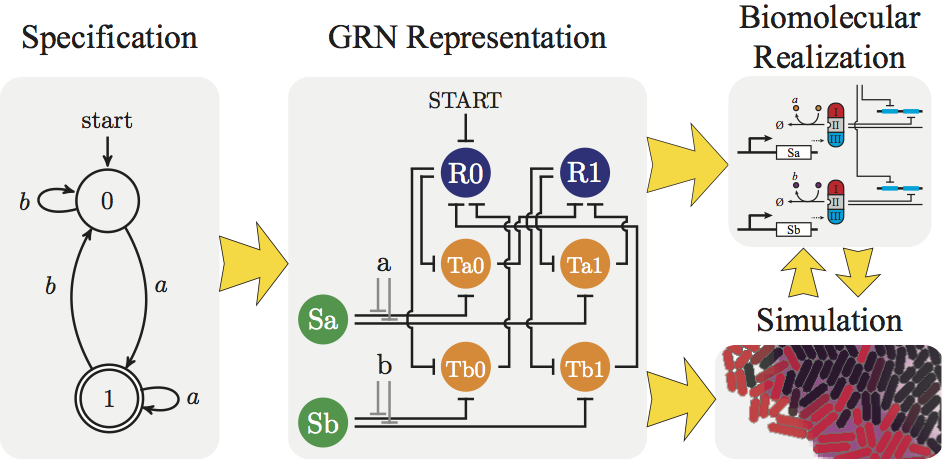
Computation in Cells and Growing Microcolonies
Finite state machines are fundamental computing devices at the core of many models of computation. In biology, finite state machines are commonly used as models of development in multicellular organisms. However, it remains unclear to what extent cells can remember state, how they can transition from one state to another reliably, and whether the existing parts available to the synthetic biologist are sufficient to implement prespecified finite state machines in living cells. Furthermore, how complex multicellular behaviors can be realized by multiple cells coordinating their states with signaling, growth, and division is not well understood. I describe a method by which any finite state machine can be built using nothing more than a suitably engineered network of readily available repressing transcription factors. In particular, I show the mathematical equivalence of finite state machines with a Boolean model of gene regulatory networks. I describe how such networks can be realized with a small class of promoters and transcription factors. To demonstrate the robustness of our approach, I show that the behavior of the ideal Boolean network model approximates a more realistic delay differential equation model of gene expression. Finally, I explore a framework for the design of more complex systems via an example, synthetic bacterial microcolony edge detection, that illustrates how finite state machines could be used together with cell signaling to construct novel multicellular behaviors.
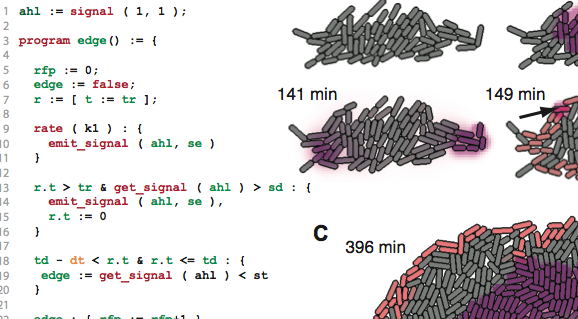
Simulating and Specifying Multicellular Behaviors
Recent advances in the design and construction of synthetic multicelled systems in E. coli and S. cerevisiae suggest that it may be possible to implement sophisticated distributed algorithms with these relatively simple organisms. However, existing design frameworks for synthetic biology do not account for the unique morphologies of growing microcolonies, the interaction of gene circuits with the spatial diffusion of molecular signals, or the relationship between multicelled systems and parallel algorithms. We developed gro, a framework for specifying and simulating multicellular behaviors that uses a simple 2D simulation of microcolony growth and molecular signaling. The framework allows the researcher to explore the collective behaviors induced by high level descriptions of individual cell behaviors.
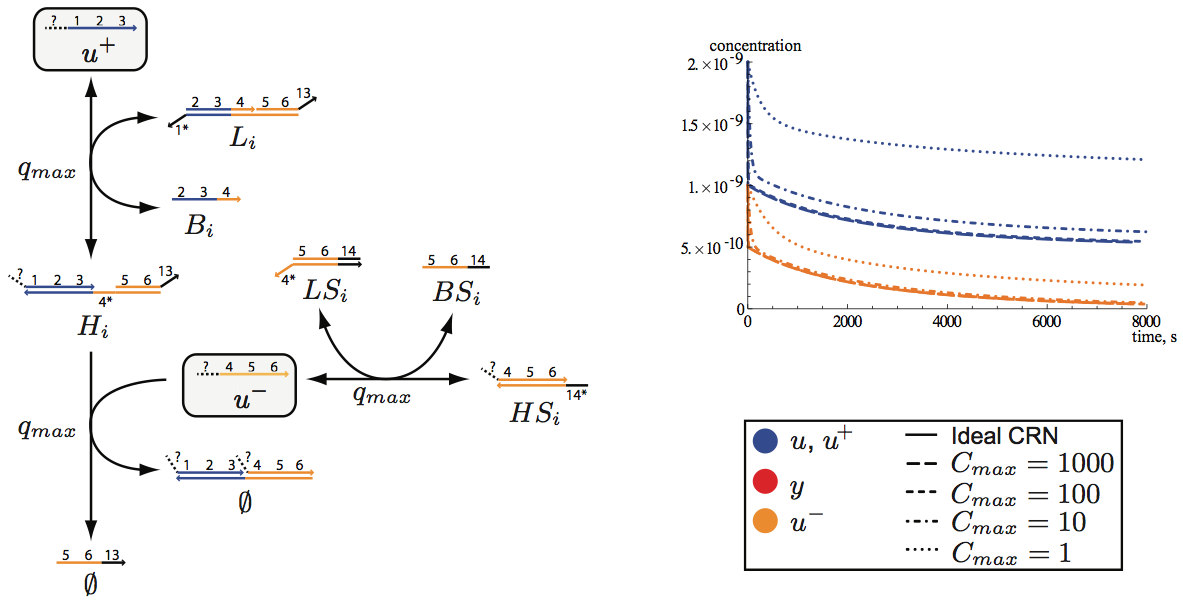
DNA Programming
Linear I/O systems are a fundamental tool in systems theory, and have been used to design complex circuits and control systems in a variety of settings. Here I present a principled design method for implementing arbitrary linear I/O systems with biochemical reactions. This method relies on two levels of abstraction: first, an implementation of linear I/O systems using idealized chemical reactions, and second, an approximate implementation of the ideal chemical reactions with enzyme-free, entropy-driven DNA reactions. The ideal linear dynamics are shown to be closely approximated by the chemical reactions model and the DNA implementation. I illustrate the approach with integration, gain and summation as well as with the ubiquitous robust proportional-integral controller.
Dynamic Legged Climbing (Masters Thesis)
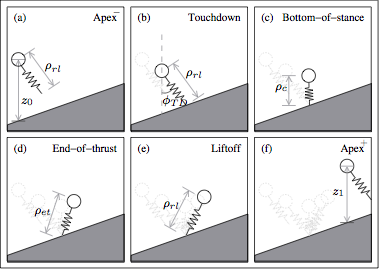
Stability and Control for a Class of Dynamic Legged Climbers, May 2006.
Motivated by the success of the lateral leg spring (LLS) and spring-loaded inverted pendulum (SLIP) templates for transverse and sagittal plane running on horizontal surfaces, my effort is to similarly approximate the analytically intractable dynamics of a full dimensional system through planar models, and develop simple control strategies based on analysis of these approximations. In this report I introduce low-dimensional generalizations of the LLS and SLIP templates capable of ascending and descending by considering configurations of the center of pressure outside of the set of asymptotically stable configurations in the horizontal plane, and allow a thrust phase to add or remove energy from the hopper. I provide mathematical analysis of these models where possible, and introduce approximate models and empirical data where analytical analysis is intractable. Stable control strategies developed from these low dimensional templates and approximations are demonstrated through simulation.
Past Research and Other Projects
- 2005, Linear and Nonlinear Dimensionality Reduction in fMRI Data for Picture-Sentence Classification (with Stuart Anderson).
- 2002-2004, Urban Search and Rescue: Cyber Agents, Robots and People (advisors Illah Nourbakhsh, Katia Sycara, Mike Lewis).
- 2004, Development of an Automatic Bicycle Shifting System and Associated Human Interfaces (with Stuart Anderson and Michael Blain).